Geometric data analyis, beyond convolutions

I defended my PhD thesis on July 2nd, 2020: a video recording is available here. My thesis is the best introduction to my work: it is written as a textbook for data sciences and shape analysis, from a geometric perspective. If you just saw one of my talks on symbolic matrices and large-scale optimal transport, here is what you are looking for: KeOps library, GeomLoss package, Slides for the defense, PhD thesis.

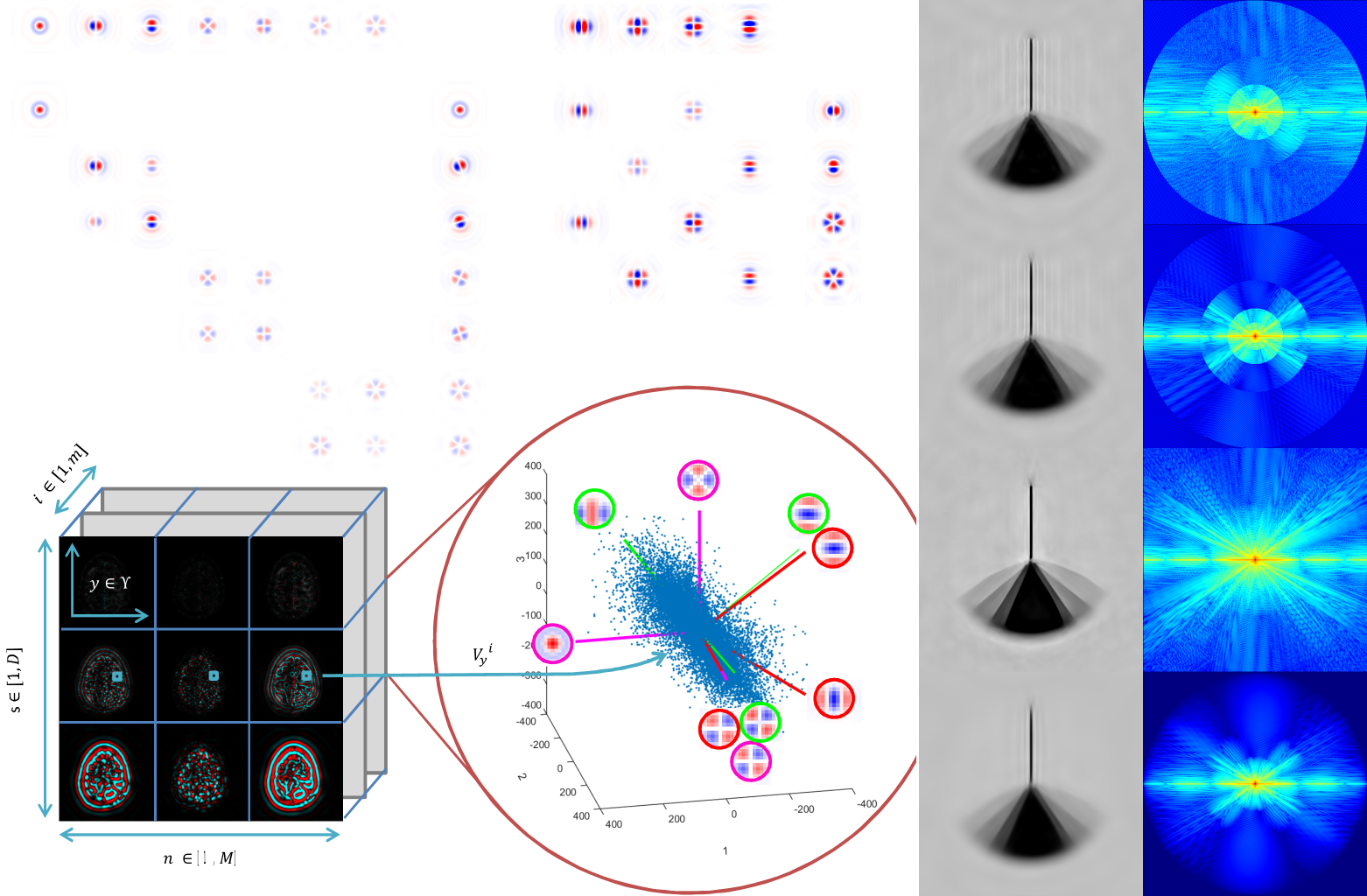
Fast geometric learning with symbolic matrices

Since September 2017

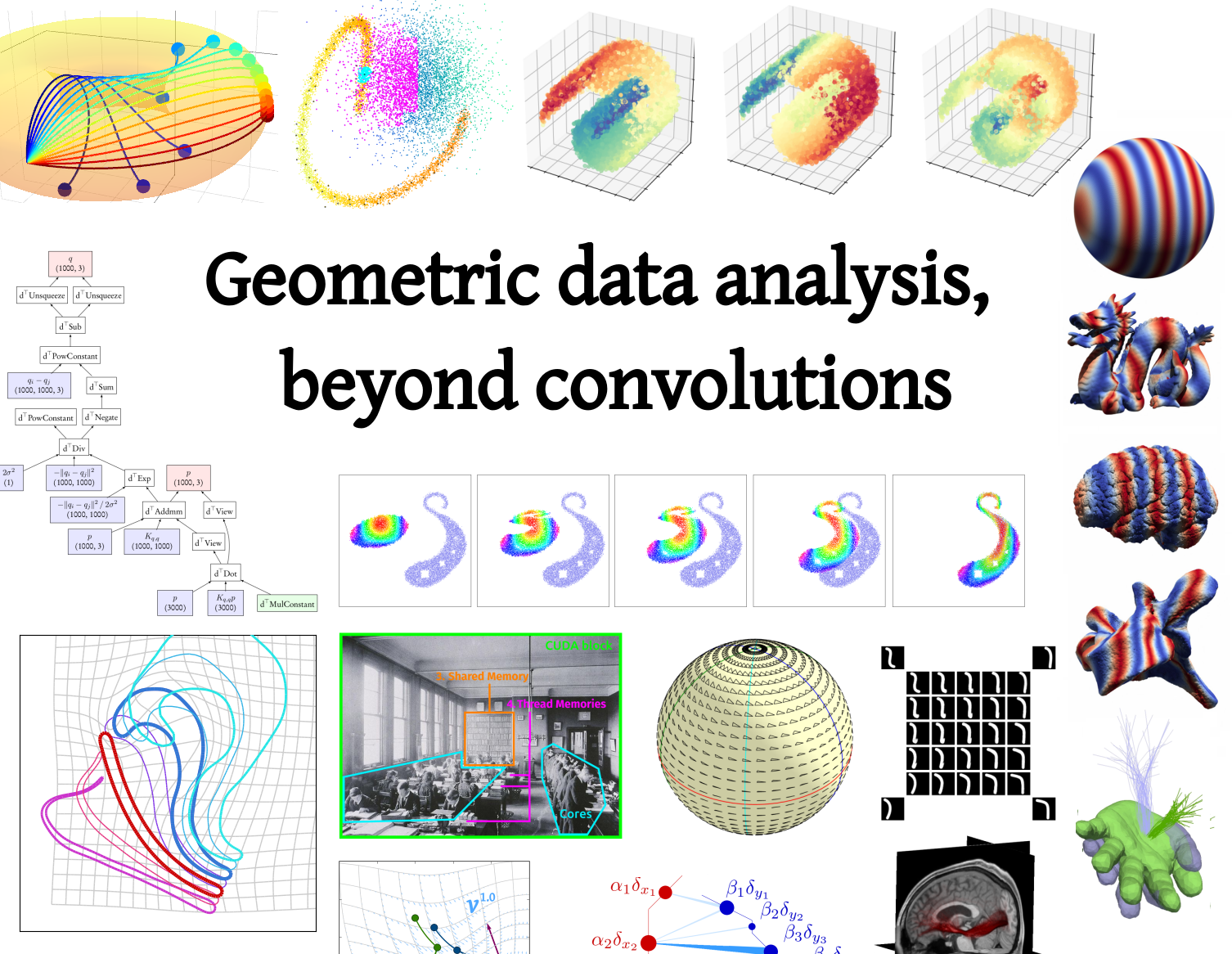
Scientific computing tools have a major influence on the research landscape. Over the years, frameworks such as Fortran, Matlab, NumPy, TensorFlow or PyTorch have put a focus on linear operations (matrix products, convolutions, Fourier transforms...) and thus biased research in applied mathematics towards Euclidean models and geometries. This creates an unfortunate situation where researchers have to compromise between computational speed and modelling freedom.

A significant part of my work is to break through this software bottleneck. As part of the KeOps developement team, I develop extensions for Python and R that ease the development of geometric algorithms, especially for methods that rely on distance or kernel matrices.

Our KeOps package speeds up geometric computations by several orders of magnitude and comes with all the desirable features of a modern library (GPU support, automatic differentiation...). It has been downloaded more than 100k times as of 2022. We are now working to make it standard in several applied fields, from survival analysis to geometric deep learning. To get started, here is a collection of useful links:

• Automatic differentiation for applied mathematicians, introductory slides if you've never heard about PyTorch.
• Our NeurIPS paper and spotlight presentation for a quick overview.
• Fast geometric libraries for vision and data sciences, a longer talk that focuses on 3D applications.
• www.kernel-operations.io, our website. Note that KeOps is easy to install with pip!

Computational optimal transport

Since December 2016

Optimal transport generalizes sorting to spaces of dimension D > 1. It is especially useful in shape analysis (where it replaces advantageously the nearest neighbor projection) and in data sciences (to re-order samples and match them with each other). Going further, it induces the "Wasserstein" or "Earth Mover's" distance between probability distributions that allows researchers to inject structuring geometric priors into machine learning pipelines.

As part of a dynamic community centered around the MoKaPlan Inria team in Paris, Gabriel Peyré's lab at the ENS and the POT development team in Saclay, I work on turning this fundamental mathematical concept into a standard tool for data sciences. Notably, I have provided key robustness guarantees for the smooth Sinkhorn divergences and develop the fastest transport solver available online, GeomLoss. You may be interested by:

• Introductory slides and poster. A good starting point if you have a background in computer graphics, image processing or machine learning.
• Tutorial on gradient flows (+source). A notebook that showcases the typical behaviours of kernel norms (aka. Maximum Mean Discrepancies), Maximum Likelihoods of Mixture Models (aka. weighted Hausdorff distances) and Optimal Transport costs in model-fitting applications.
• Chapters 3 and 4 of my PhD thesis, that provide an accessible overview of the topic from a geometric and computational perspective, in complement of this excellent textbook by Peyré and Cuturi.
• Geomloss: a reference implementation that scales up to millions of samples and is available through pip.

My papers on the topic:

• Optimal transport for diffeomorphic registration (2017), our first proof-of-concept paper on the subject, selected for oral presentation at MICCAI 2017.
• Global divergences between measures: from Hausdorff distance to optimal transport (2018), an introduction focused on shape analysis and computer graphics.
• Interpolating between optimal transport and MMD using Sinkhorn divergences (2018), my main theoretical contributions on Sinkhorn divergences.
• Sinkhorn divergences for unbalanced optimal transport (2019), an extension to positive distributions (that may not have the same mass) by Thibault Séjourné.
• Fast and scalable optimal transport for brain tractograms (2019), a first application to neuro-anatomy.
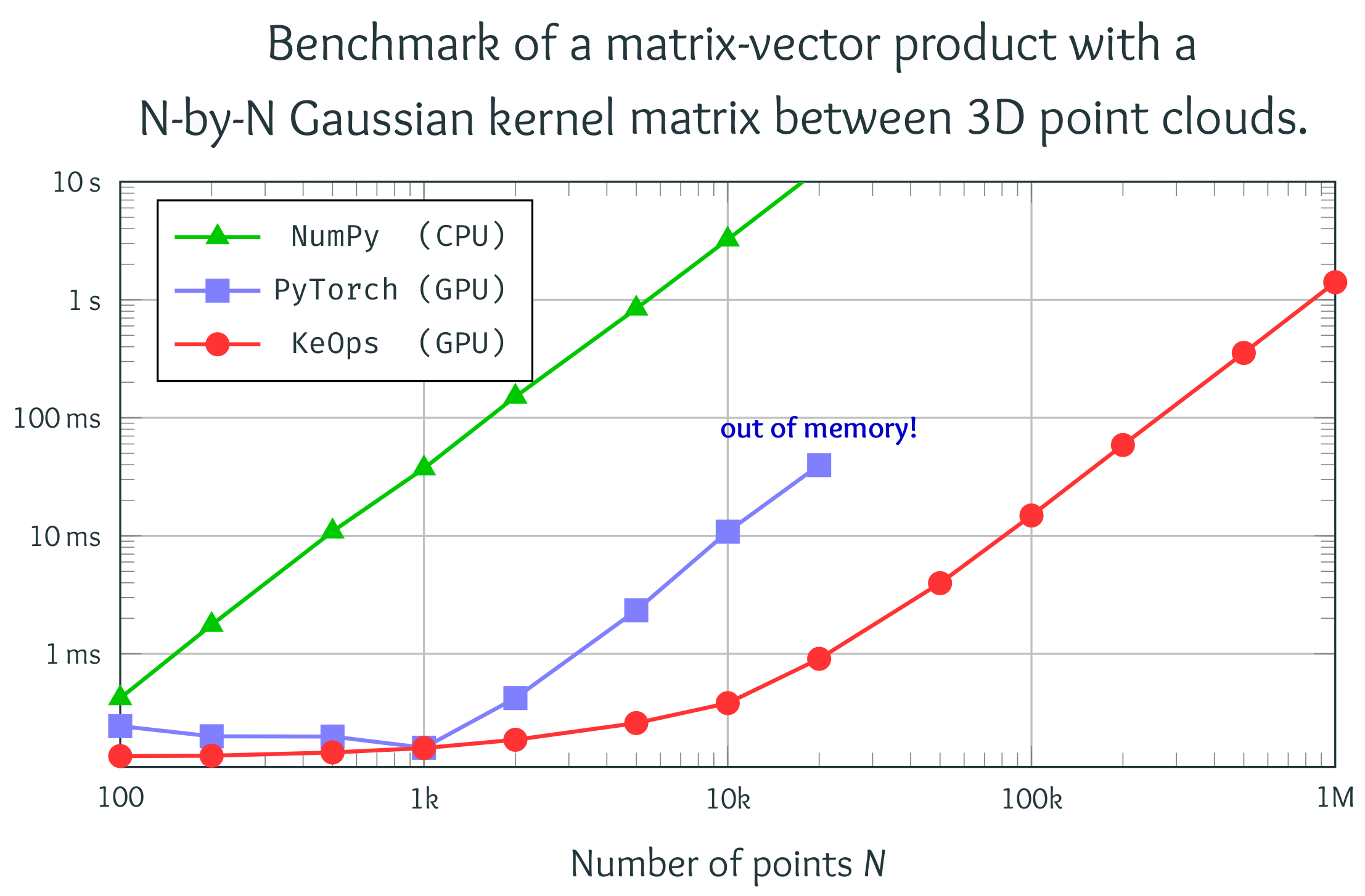
• Accurate point cloud registration with robust optimal transport (2021), a mature discussion of applications to 3D shape analysis with a focus on 3D scene flow and lung registration (see image below).

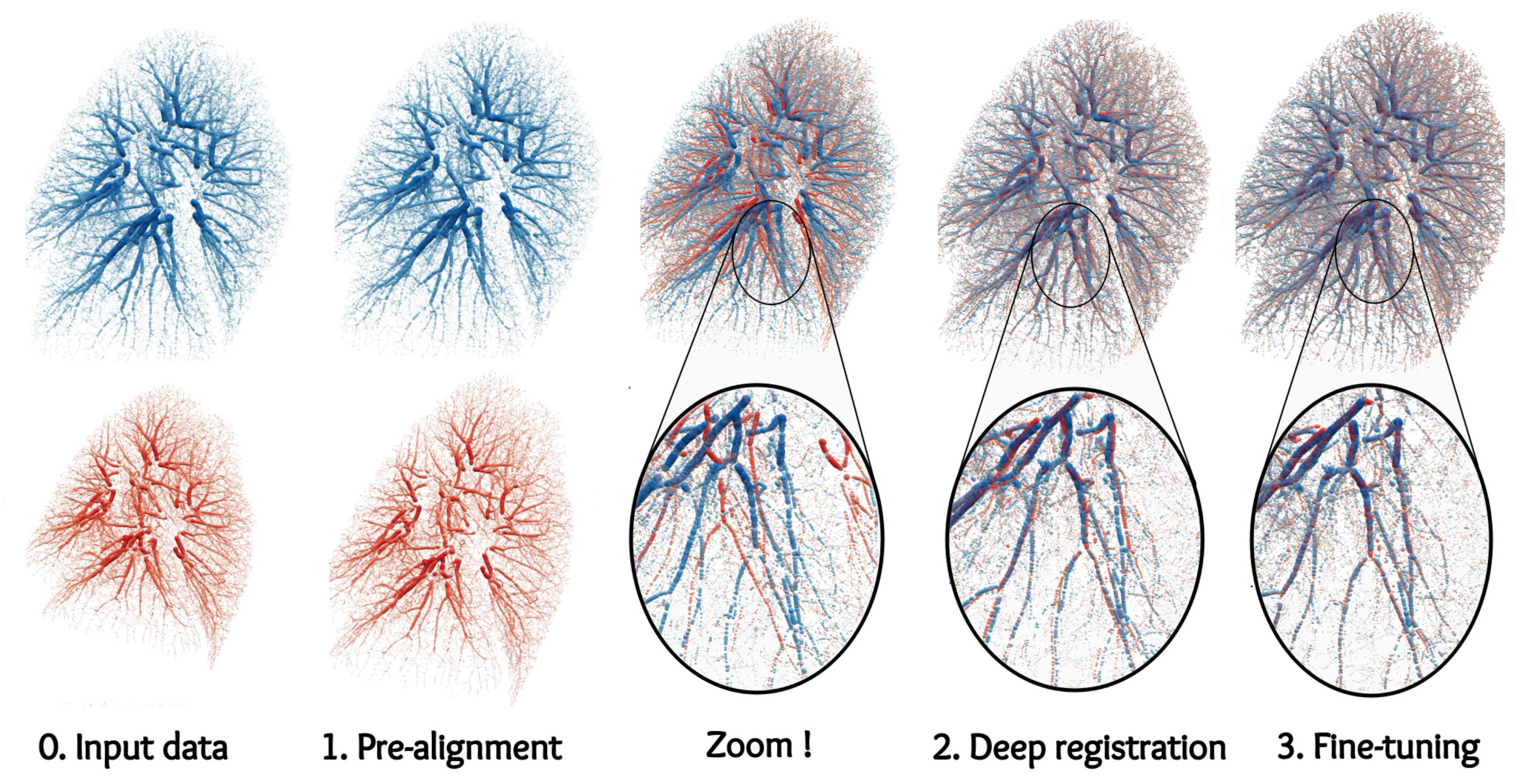
Protein docking

Since January 2020

Protein docking is a fundamental problem in biochemistry, where one tries to predict how two large molecules may bind to each other in 3D space. I worked on this topic as part of a joint EPFL-Imperial team in close collaboration with Freyr Sverrisson. We developed a scalable and principled geometric deep learning model to tackle this question, as described in the following papers:

• Deciphering interaction fingerprints from protein molecular surfaces using geometric deep learning (2019), the first paper of our team on this topic, published before my arrival.
• Fast end-to-end learning on protein surfaces (2021), that introduced our KeOps-based method.
• Physics-informed deep neural network for rigid-body protein docking (2022), an extension of the work above that directly predicts a distribution of plausible docking configurations.

Steerable Wavelets for Medical Image Denoising

Summer 2015

My master's thesis was written during a 5-months long internship at Siemens CT/Healthcare in Princeton, NJ. I attempted to build on the work of Michael Unser and Nicolas Chenouard on steerable wavelets to improve the real-time denoising pipeline used in Siemens scanners and fluoroscopic devices.

Unfortunately, I signed a non-disclosure agreement which prevents me from putting my master's thesis online : as a consolation, here is a short "Introduction to a Research Topic" written to introduce my fellow ENS classmates to medical image denoising - in french.

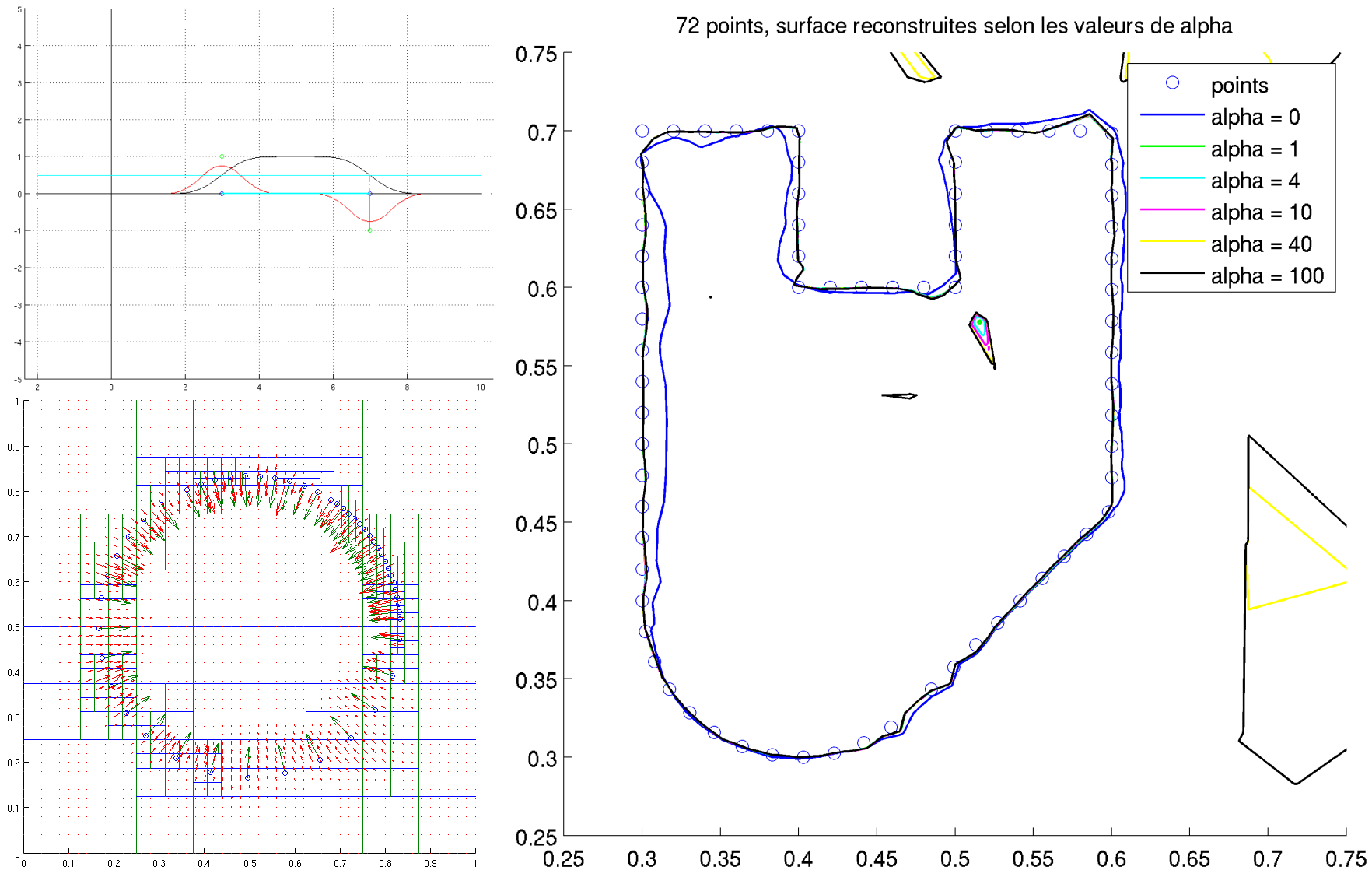
Screened Poisson Surface Reconstruction

March 2015

In order to complete the Points Clouds and 3D Modeling MVA course by François Goulette, Jean-Emmanuel Deschaud and Tamy Boubekeur, I worked on the Screened Poisson surface reconstruction algorithm proposed in 2013 by Michael Kazhdan and Hugues Hoppe, eventually implementing it from scratch in the 2D Euclidean plane.

My report can be found here, as well as the Matlab code and the beamer presentation.

Gradient Lines Drawing

January-February 2015

This is the project Vincent Vidal and I worked on for our MVA course: Sub-pixel Image Processing, by Lionel Moisan. Left free to design our own experiments and methods, Vincent and I wrote a comparative study on the methods to compute and visualize the gradient lines of an image.

Our report can be found here, as well as the code.

SIFT Flow : Find the Difference !

January 2015

I did this project with Vincent Vidal for the MVA course: Object Recognition and Computer Vision, by Jean Ponce, Ivan Laptev, Cordelia Schmid and Josef Sivic. Using the EECV 2008 SIFT Flow algorithm, we designed a way to compare two pictures of the same building detecting occlusions, deformations and drawing errors regardless of variations in graphic style.

Our report can be found here, as well as the code.

Vocoder

May 2013

As part of my signal processing course at the École Normale Supérieure, Li-Yao Xia and myself wrote a small "Vocoder" using Matlab. This program is able to modify the speed rate of a sound file without altering its pitch, following a method given in this paper by Michael R. Portnoff. A complete analysis of our results can be found here (in French). I very much enjoyed "debugging" this program, testing and comparating various convolution windows.

Just a little example of what we achieved : a short excerpt from this video, followed by a speeded up version :

MiniC compiler

December 2012

As part of my compilers course at the École Normale Supérieure, Ken Chanseau Saint-germain and myself wrote in OCaml a MiniC (fragment of C) to MIPS assembly compiler. I found it extremely pleasant to understand the underlying constraints of programming languages such as C (for instance, I eventually understood how recursive functions or multiple inheritance were actually implemented).

Eventually, our MiniC compiler was able to compile and execute this Mandelbrot set drawing program, resulting in this MIPS assembly code, and the following output :

Maths Courses to Trees

2011-2013

Inspired by infographics books and innovative works such as Oliver Byrne's "The Elements of Euclid" (a must-have for every mathematician), I decided that I would publish a mathematics textbook suiting my own taste... someday!

A first step would be to turn a Latex course into a mindmap. Consequently, I coded a little software that turns an XML version of the course into a good-looking "inferencial" tree, using Graphviz, PGF/Tikz and dot2tex. As an example, here is a tree I actually used for my studies :

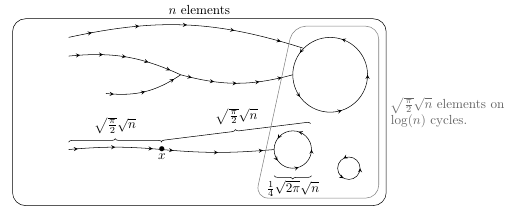
Random and Discretized Mixing Maps

2012-2013

As part of my studies at the École Normale Supérieure, Alexis Gilles and myself wrote a memoir which is entitled "Random Permutations and Discretization of Mixing Maps" : Does the sampling of a mixing map produce a generic map ? Is it possible to infer properties of the continuous map from the discretized one ?

The paper features theorems and analysis of the statistics that I computed, our theoretical framework being the reduction modulo p of a polynomial with integer coefficients.

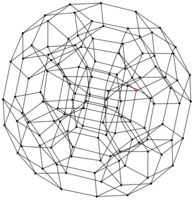
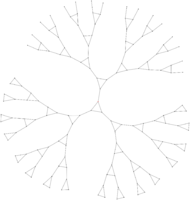
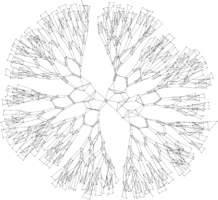
Hyperbolic groups are Automatic

2011

As a preparation to the competitive exam for entry to the École Normale Supérieure, I wrote a memoir on a subject at the border between geometric groups theory and computer science : Automatic and Hyperbolic groups. In a nutshell, considering a finitely generated group and its Cayley graph, we prove that if triangles in the graph are "slim" in Gromov sense, then the structure of the graph can somehow be described with regular expressions.

Here is a link to a summarized version of the work I did. By way of experiments, using this little OCaml program I coded and Graphviz, I computed several dozens of Cayley graphs (see below a few of them).